
- #Improper Integral Calculator Series Of Pure
- #Improper Integral Calculator Free Online Tool
- #Improper Integral Calculator How To Solve Equations
Improper Integral Calculator How To Solve Equations
To approximate the R b a f(x)dx, we again subdivide the interval into n subintervals of equal. First, we must recall the area of a trapezoid. 2 4 6 8 10 x 1 2 3 y=ecos(x) The Trapezoid Rule uses trapezoids rather than rectangles to estimate de nite integrals. Using the Midpoint Rule with n = 5 subdivisions, approximate R 10 0 e cosx dx. How to convert a mixed fraction into a decimal, formula for a square, abstract algebra tutorial, ti 83 entering base log, how to solve equations with a number and a fraction, is a square root an expression. Finding slope on a ti-84 calculator, 8 bit binary calculator, fractions and square root calculator, 9th grade printible math worksheets.
Improper Integral Calculator Free Online Tool
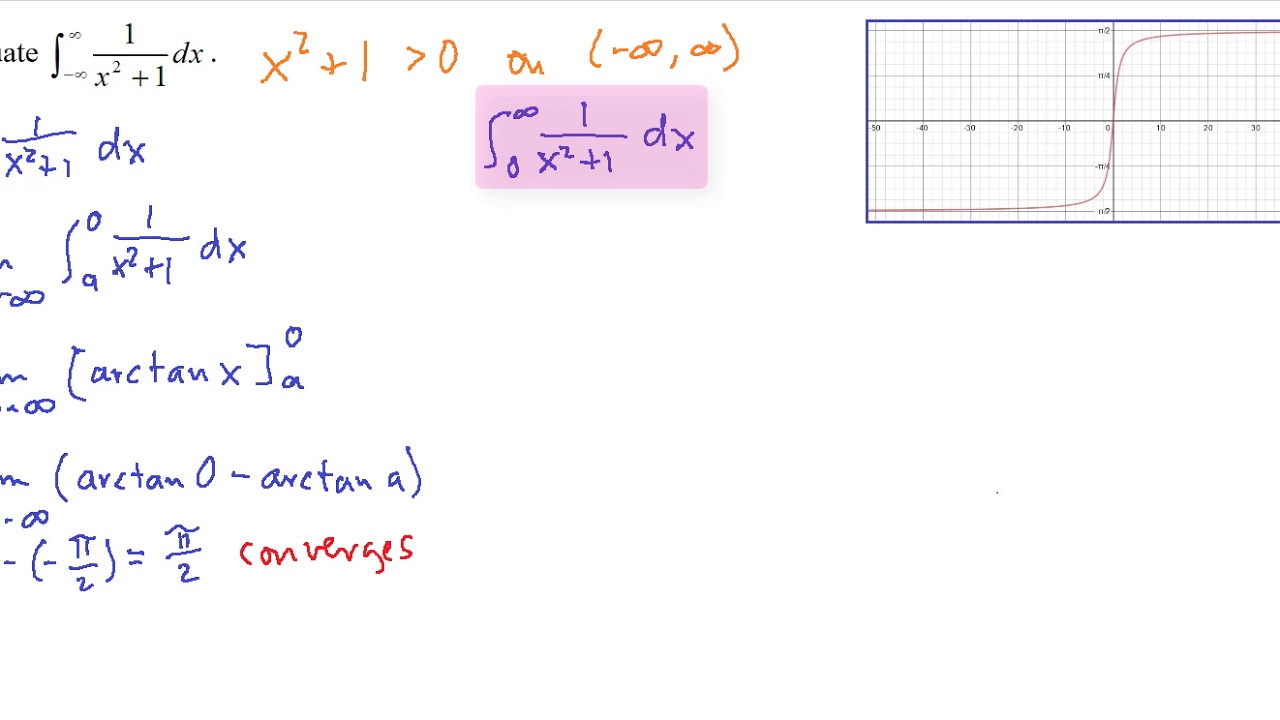
Use proper limit notation. The formal rule is given by The formal rule is given by ∫ a b f ( x ) 𝑑 x ≈ h 2 Improper Integral Calculator is a free online tool that displays the integrated value for the improper integral. The trapezoidal rule is a method for approximating a definite integral by evaluating the integrand at two points. See a step-by-step solutionImproper Integrals To this point we have only considered integrals R b a f(x) dx with the limits of integration a and b nite and the integrand f(x) bounded (and in fact continuous except possibly for nitely many jump discontinuities) An integral having either an innite limit of integration or an unbounded integrand is called. In a moment you will receive the calculation result. Type in the indefinite integral problem to solve To get started, type in a value of the indefinite integral and click «Submit» button.

The Maple student package has commands for visualizing these three rectangular area approximations. In particular, we will consider the left, right and midpoint rules. Hello, I took an entry level Matlab course last semester and for a Calculus 2 assignment I have to write a program to find the left,right,and midpoint rule as well as simpson's rule and the trapezoidal rule.
How can I use the TI83 calculator to generate a graph of an antiderivative of f(x)? 6. However, I do not have a formula for an antiderivative of f(x). I have a formula for f(x).
The midpoint rule approximates the definite integral using rectangular regions whereas the trapezoidal rule approximates the definite integral using trapezoidal approximations. Make use of Midpoint rule, Trapezoid rule and Simpson's rule to approximate an integral python python3 numerical-methods numerical-integration simpson-rule calculus-2 trapezoidal-method midpoint-method When you use Maple for integration, you need not use the rule for evaluating integrals. (1.1.5) (1.1.4) (1.1.1) (1.1.2) (1.1.6) (1.1.3) Chapter 7 TECHNIQUES OF INTEGRATION 7.1 Integration by Part Integration by parts formula.
Integral (1/ln(t) dt), upper limit 3, lower limit 2, n=10 use the trapezoidal rule, the midpoint rule, and simpsons rule to approximate the given integral with the specific value of n. Notes: Trigonometric functions are evaluated in Radian Mode. Please enter a function, starting point, ending point, and how many divisions with which you want to use Riemann Midpoint Rule to evaluate. This calculator will walk you through approximating the area using Riemann Midpoint Rule.
The Midpoint Rule, and Simpson's rule to approximate the integral with. Get the detailed answer: Use the Trapezoidal Rule. We look at a single interval and integrate by. As usual, let h = b−a n and xi = a+ih. Suppose we want to estimate Rb a f(x)dx using the Trapezoidal Rule with n intervals. (The Midpoint Rule is, too — see exercises at the end.) We do that here.
Improper Integral Calculator Series Of Pure
Calculate a table of the integrals of the given function f(x) over the interval (a,b) using Trapezoid, Midpoint and Simpson's methods. It’s best not to use this method if the number of integration points is limited. As you can imagine, this results in poor accuracy when the integrand is changing rapidly. The midpoint rule estimates the area under the curve as a series of pure rectangles (centered on the data point).
Consider a formula that takes the value y = b(x) over an interval of x1 to x2, where x2 is equal to x1 + h. The midpoint rule of calculus has several general steps. It is calculated by increasing the number of partitions to double from 2 to N.
It is certainly useful to know how accurate an approximation is. Error Bounds for Midpoint and Trapezoidal approximations. Approximate \(\int_0^4(4x-x^2)\ dx\) using the Right Hand Rule and summation formulas with equally spaced intervals. Example 5.3.10 Approximating definite integrals using sums. The following example lets us practice using the Right Hand Rule and the summation formulas introduced in Theorem 5.3.9. The midpoint rule with these values is equal to hf (x1 + h/2).
It follows that ∫ ≈ (−) ⋅ + (). The trapezoidal rule works by approximating the region under the graph of the function as a trapezoid and calculating its area. Simpson's rule approximates the definite integral by first approximating the original function using piecewise quadratic functions. The midpoint rule approximates the definite integral using rectangular regions whereas the trapezoidal rule approximates the definite integral using trapezoidal approximations.



 0 kommentar(er)
0 kommentar(er)
